Because I hang out with atheist student groups, the Bible comes up every so often. My official position on the Bible is that it's more boring than The Lord of the Rings. I tell people this as a way of changing the subject--many atheists just won't let go of the implication that The Lord of the Rings is awful--and as a way of reminding people that there is no accounting for taste.
Oh, but underneath the talk, there is accounting for my taste. I know why I feel the Bible is boring. It has to do with my Catholic upbringing.
Catholics are known deemphasizing the Bible, as compared to protestants. This makes historical sense, since Protestantism was caused by the printing press and mass literacy. And I think it's generally true today, or at least it's been true in my experience. I never owned a copy of the Bible. As a kid, I never read it.
As a kid, I only ever heard Bible readings during the Catholic Mass. Catholic Masses are said to be particularly boring among Christian services. I myself was so bored by Mass that eventually I refused to go against the will of my mother, many years before I quit Catholicism. It didn't help that when I was young I had auditory processing difficulties, made all the worse by the echoing acoustics of a Catholic church. I could maybe understand the Bible readings if I focused really hard, but what was the point? It was all so boring and pointless, like the rest of Mass.
When I was older, I did read parts of the Bible. I went to a Jesuit high school, and we had a class in scripture. We didn't read the whole thing, just bits and pieces considered important in Catholicism. For the most part, we learned about the general structure, and what various books were about. I don't remember much of it. I remember the motivations of the different gospels, and I remember a few of Jesus' parables. Mostly I remember it being incredibly boring, just like nearly every other book we read in high school.
Dear readers, did any of you have the same experience of hating nearly every book you read in high school? It seems to be a common experience, though I'm not sure why. Is it because teenagers just don't appreciate the kind of books that English teachers think are edifying? Is it because the reading is forced? Whatever the reason, I felt that way about the Bible. This isn't entirely rational, of course. I'm sure there are some books I read in high school that I could read again and discover that they were quite decent all along. But in the Bible's case, I'm sure I would still find it terrible.
For one thing, I know that what I saw in high school were the "good" parts of the Bible. It can only get worse from there
For another thing, what I know about the Bible just doesn't line up with my taste in reading. I don't like reading "so bad it's good" stuff. I generally don't like "classic" literature. I don't think it is important to recognize cultural references to classic literature (what good does that do for me or for society?), and anyway I already recognize most Bible references because of my education. What I like in a book is willingness to criticize itself and its own messaging. I also like books that focus on the subtleties and ironies of modern social interactions--not really the kind of thing that translates across millenia?
Some atheists will argue at length about what is the "correct" interpretation of the Bible, mostly so they can accuse various Christians of not following it. Sometimes I think these arguments are a bit sketchy (but no more so than Christian interpretations), but mostly I just don't care. There may be some utility to such an argument, but since I have no interest in investing the time, I prefer to argue that it doesn't matter. The Bible isn't an authority on what's right, nor on what's wrong, so a person's degree of faithfulness to the Bible is irrelevant to my moral approval. I don't even consider faithfulness to the Bible to be a measure of religiosity or Christian-ness. After all, I came from a Catholic background, where the Bible was deemphasized, and I don't think Catholics are any less Christian for it.
Saturday, November 30, 2013
Thursday, November 28, 2013
Why video games are so flammable
With Black Friday upon us, the flame wars over next-gen gaming consoles have really been heating up. Which will win: the Wii U, XBox One, or PlayStation 4? No one truly knows, but gamers everywhere agree that everyone else is wrong and should feel bad about being so stupid.
While I don't intend to make a habit out of discussing economics, I do think that video game flame wars can be understood within economics. The problem is twofold:
Video game console producers have even more reason to be large. Besides the large development costs of video game consoles, gamers also want consoles with games on them (especially games exclusive to that platform). Consoles won't get many games unless there are many consoles to go around. Whenever game developers port a game to a console, or make a console-exclusive game, their market is restricted by the number of console owners out there.2
The important number here is the ratio of the optimal size of the video game industry to the optimal size of a video game or video game console. For consoles, that number appears to be 3-5. For games, it's much larger, but still noticeably discrete if you focus on major companies.
The second problem is that video games are in a state of monopolistic competition. That means that the products of different companies are all different, and are not perfect substitutes for one another. Thus different consumers might have different preferences.
This puts consumers in a sort of Battle of the Sexes game. The best outcome to a consumer is if they buy the games and consoles they want, and everyone else follows even if it's not what they most want. But if everyone buys something else, the consumer has to choose between buying what they want (even though a worse-selling product will suffer in value) and buying what everyone else is buying. People don't like being in this situation, and it's clear whose fault it is: other consumers! Flaming those people may vent anger, and also persuade more consumers to one's own side.
There are, of course, other causes as well. Video game consumers are particularly well-informed. Also I think people just like flame wars.
It will be interesting to see how the games industry changes over time. Development and advertisement costs may go down. The market may expand to include a wider array of consumer tastes. Porting games between platforms may get easier. How will this affect the number and size of video games?
------------------------------------------------
1. In a list of the most expensive video games, older games spent a lot on manufacturing, but more recent ones spend on development and advertising. For example, GTA V (2013) spent 51% of its budget on development,, 45% on advertising, and only 3% on manufacturing.
2. Any smaller consoles face these difficult problems. This is why people often mock consoles like the Ouya or Mojo.
While I don't intend to make a habit out of discussing economics, I do think that video game flame wars can be understood within economics. The problem is twofold:
- There is limited space for video games and video game consoles, and everyone knows it.
- Video games are in a state of monopolistic competition.
Video game console producers have even more reason to be large. Besides the large development costs of video game consoles, gamers also want consoles with games on them (especially games exclusive to that platform). Consoles won't get many games unless there are many consoles to go around. Whenever game developers port a game to a console, or make a console-exclusive game, their market is restricted by the number of console owners out there.2
The important number here is the ratio of the optimal size of the video game industry to the optimal size of a video game or video game console. For consoles, that number appears to be 3-5. For games, it's much larger, but still noticeably discrete if you focus on major companies.
The second problem is that video games are in a state of monopolistic competition. That means that the products of different companies are all different, and are not perfect substitutes for one another. Thus different consumers might have different preferences.
This puts consumers in a sort of Battle of the Sexes game. The best outcome to a consumer is if they buy the games and consoles they want, and everyone else follows even if it's not what they most want. But if everyone buys something else, the consumer has to choose between buying what they want (even though a worse-selling product will suffer in value) and buying what everyone else is buying. People don't like being in this situation, and it's clear whose fault it is: other consumers! Flaming those people may vent anger, and also persuade more consumers to one's own side.
There are, of course, other causes as well. Video game consumers are particularly well-informed. Also I think people just like flame wars.
It will be interesting to see how the games industry changes over time. Development and advertisement costs may go down. The market may expand to include a wider array of consumer tastes. Porting games between platforms may get easier. How will this affect the number and size of video games?
------------------------------------------------
1. In a list of the most expensive video games, older games spent a lot on manufacturing, but more recent ones spend on development and advertising. For example, GTA V (2013) spent 51% of its budget on development,, 45% on advertising, and only 3% on manufacturing.
2. Any smaller consoles face these difficult problems. This is why people often mock consoles like the Ouya or Mojo.
Thursday, November 21, 2013
Tuberose
Meenakshi Mukerji's Tuberose.
This is one of the prettiest models I have. Each module, rather than being a flat polygon, is a spiky flower shape. It works especially well with Harmony paper, which is a brand of origami paper produced by Grimmhobby that has color variations across the paper. There is no coloring pattern: each of the twelve modules is uniquely colored.
If I may ramble about my origami paper, I have a few different brands, and it's surprising how different they can be.
Harmony paper is great, but the color scheme doesn't work for just any model. It also feels like the paper is slightly rectangular (!). Grimmhobby's washi chiyogami (seen here) is very pretty, but noticeably thicker than other paper, which makes it hard to fold. I have some paper made by Daiso Japan (seen here) which is easy to fold, but has a noticeable grain in one direction. And for some reason it's harder to reverse folds. Lastly I have paper from a German company, Folia Bringmann. The colors are very bold (and both sides are colored), but I'm sorry to say that the colors fade over time.
These are things you start to notice when you make models out of thirty squares or so. If I had to buy more paper I'm not sure what I'd buy--they all have their strengths and weaknesses.
Tuesday, November 19, 2013
In which I think about monopolies
This is part 2 of my previous post.
Why, in a competitive market, are the quantity and price at the intersection of supply and demand? The answer is that buyers and sellers are not monolithic entities. As long as the price is above the intersection, a new seller can make money by producing new goods at the marginal cost and selling at the marginal value, even though this lowers the price, resulting in net losses for other sellers. As long as the price is below the intersection, a new buyer can produce value by paying more for goods, even though this makes it more expensive for all other buyers.
On the other hand, if sellers really are a monolithic entity, then we have a monopolistic market rather than a competitive one. Under monopoly conditions, the single seller may not wish to sell as much, since whenever the prices decreases, they eat all the losses themselves.
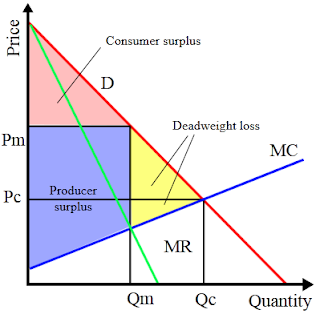
The single seller is free to set the price such that their utility US(p,q) is maximized. The constraint is that they cannot sell more than buyers demand. US is defined for all p and q, but we want to determine the maximum US specifically along the demand curve (which as I explained previously, is the same as the marginal value curve).1 $$\frac{\mathrm{d} \text{US}}{\mathrm{d} q}|_{p=\text{MV}(q)} = 0$$ $$\frac{\mathrm{d} \text{US}}{\mathrm{d} q}|_{p=\text{MV}(q)} = \frac{\mathrm{d}}{\mathrm{d} q}(\text{MV}(q)*q) - \text{MC}(q)$$ $\text{MV}(q)*q$ is the seller's revenue, the price of goods times the total quantity sold. $\frac{\mathrm{d}}{\mathrm{d} q}(\text{MV}(q)*q)$ is therefore the marginal revenue. So in a monopoly, the quantity of goods is at the intersection of marginal revenue and marginal cost. The price of goods is set to the maximum that demand will allow. Let's look again at figure 1.
In a competitive market, the quantity and price are given by the intersection of supply and demand, or marginal cost (MC) and demand (D). In a monopoly market, the quantity is given by the intersection of marginal cost (MC) and marginal revenue (MR), and the price is given by the demand (D) curve.
I've left out analysis of a monopsony, because it's exactly the same. Instead of a single seller, there is a single buyer who chooses the price to maximize UB while constrained to the supply curve.
In the previous post, I said it was confusing that the "marginal cost" in figure 2 means something completely different from the "marginal cost" in figure 1. In figure 1, the marginal cost is the cost to the seller to produce one more unit. In figure 2, the marginal cost is the cost to a single buyer to buy one more unit (including the additional cost from prices being raised).
Next I want to discuss "deadweight loss", which is the sum total utility (of both the buyers and sellers) lost compared to a competitive market. When people trade goods for money, both the buyers and sellers benefit. For the buyer, the goods have more value than the money paid. For the seller, they are paid more than it cost to produce the good. I already showed this in my previous post when I gave expressions for utility functions UB and US. However, it helps to have a graphical interpretation of the utility.
First, consider the buyer (figure 3a). The total value of the goods to the buyer is given by the area under the marginal value curve (red). But to get the total utility we must also subtract off the price paid for the goods (blue). Next consider the seller (figure 3b). The cost of production is given by the area under the marginal cost curve (green). The utility to the seller is equal to the total price paid to buy the goods (blue) minus the total cost to produce them (green).
In figure 1, the utility to buyers is shown in red (consumer surplus), while the utility to sellers is shown in blue (producer surplus). Relative to a competitive market, a monopoly has two effects. First, the producer gets more utility while the consumer gets less. Second, the sum utility is smaller, by an amount shown by the yellow "deadweight loss" area.
Now that I've learned about the concept of deadweight loss, I understand a bit why some people think a "free market" is best (although clearly there need to be restrictions on monopolies, so I think "free" is a misnomer). But given that this is only the simplest market imaginable, it's not clear that it generalizes to more realistic markets.
Even in this simplest case, I question the meaningfulness of the "total utility". I think, for instance, there is some intrinsic utility to a more fair or more even distribution of wealth. The distribution of wealth that results from a competitive market basically bears no relation to what is fair.
And there's another problem that comes from the initial uneven distribution of wealth. The utility to the consumers is not measured directly, but implied by how much money consumers are willing to spend. But if you think about why some consumers are less willing to pay for a good, it's not necessarily because they derive less value from the good. Often it's because they are poorer, and therefore place a higher utility value to the dollar. Thus the utility to the buyers is not equal to the amount of money they would pay. It only seems that way if you convert utility to dollar units, ignoring that dollar units are larger to some people than to others.
One way you can fix the problem is by redistributing all wealth evenly. I think there might be a few kinks in that particular solution though...
----------------------------------------
1. This illustrates a mathematical distinction between derivatives and partial derivatives. When we have a function of two variables, like US(p,q), the derivative isn't uniquely defined unless we specify a particular direction in the (p,q) plane. So we restrict the (p,q) plane to a particular curve, and find the slope along that curve. The partial derivative is the slope along a p=constant curve. But here I take the derivative along the demand curve.
Why, in a competitive market, are the quantity and price at the intersection of supply and demand? The answer is that buyers and sellers are not monolithic entities. As long as the price is above the intersection, a new seller can make money by producing new goods at the marginal cost and selling at the marginal value, even though this lowers the price, resulting in net losses for other sellers. As long as the price is below the intersection, a new buyer can produce value by paying more for goods, even though this makes it more expensive for all other buyers.
On the other hand, if sellers really are a monolithic entity, then we have a monopolistic market rather than a competitive one. Under monopoly conditions, the single seller may not wish to sell as much, since whenever the prices decreases, they eat all the losses themselves.
The single seller is free to set the price such that their utility US(p,q) is maximized. The constraint is that they cannot sell more than buyers demand. US is defined for all p and q, but we want to determine the maximum US specifically along the demand curve (which as I explained previously, is the same as the marginal value curve).1 $$\frac{\mathrm{d} \text{US}}{\mathrm{d} q}|_{p=\text{MV}(q)} = 0$$ $$\frac{\mathrm{d} \text{US}}{\mathrm{d} q}|_{p=\text{MV}(q)} = \frac{\mathrm{d}}{\mathrm{d} q}(\text{MV}(q)*q) - \text{MC}(q)$$ $\text{MV}(q)*q$ is the seller's revenue, the price of goods times the total quantity sold. $\frac{\mathrm{d}}{\mathrm{d} q}(\text{MV}(q)*q)$ is therefore the marginal revenue. So in a monopoly, the quantity of goods is at the intersection of marginal revenue and marginal cost. The price of goods is set to the maximum that demand will allow. Let's look again at figure 1.
Figure 1: Monopoly
In a competitive market, the quantity and price are given by the intersection of supply and demand, or marginal cost (MC) and demand (D). In a monopoly market, the quantity is given by the intersection of marginal cost (MC) and marginal revenue (MR), and the price is given by the demand (D) curve.
Figure 2: Monopsony
I've left out analysis of a monopsony, because it's exactly the same. Instead of a single seller, there is a single buyer who chooses the price to maximize UB while constrained to the supply curve.
In the previous post, I said it was confusing that the "marginal cost" in figure 2 means something completely different from the "marginal cost" in figure 1. In figure 1, the marginal cost is the cost to the seller to produce one more unit. In figure 2, the marginal cost is the cost to a single buyer to buy one more unit (including the additional cost from prices being raised).
Next I want to discuss "deadweight loss", which is the sum total utility (of both the buyers and sellers) lost compared to a competitive market. When people trade goods for money, both the buyers and sellers benefit. For the buyer, the goods have more value than the money paid. For the seller, they are paid more than it cost to produce the good. I already showed this in my previous post when I gave expressions for utility functions UB and US. However, it helps to have a graphical interpretation of the utility.
Figure 3: Visual representation of utility to buyers (a) and sellers (b)
First, consider the buyer (figure 3a). The total value of the goods to the buyer is given by the area under the marginal value curve (red). But to get the total utility we must also subtract off the price paid for the goods (blue). Next consider the seller (figure 3b). The cost of production is given by the area under the marginal cost curve (green). The utility to the seller is equal to the total price paid to buy the goods (blue) minus the total cost to produce them (green).
In figure 1, the utility to buyers is shown in red (consumer surplus), while the utility to sellers is shown in blue (producer surplus). Relative to a competitive market, a monopoly has two effects. First, the producer gets more utility while the consumer gets less. Second, the sum utility is smaller, by an amount shown by the yellow "deadweight loss" area.
Now that I've learned about the concept of deadweight loss, I understand a bit why some people think a "free market" is best (although clearly there need to be restrictions on monopolies, so I think "free" is a misnomer). But given that this is only the simplest market imaginable, it's not clear that it generalizes to more realistic markets.
Even in this simplest case, I question the meaningfulness of the "total utility". I think, for instance, there is some intrinsic utility to a more fair or more even distribution of wealth. The distribution of wealth that results from a competitive market basically bears no relation to what is fair.
And there's another problem that comes from the initial uneven distribution of wealth. The utility to the consumers is not measured directly, but implied by how much money consumers are willing to spend. But if you think about why some consumers are less willing to pay for a good, it's not necessarily because they derive less value from the good. Often it's because they are poorer, and therefore place a higher utility value to the dollar. Thus the utility to the buyers is not equal to the amount of money they would pay. It only seems that way if you convert utility to dollar units, ignoring that dollar units are larger to some people than to others.
One way you can fix the problem is by redistributing all wealth evenly. I think there might be a few kinks in that particular solution though...
----------------------------------------
1. This illustrates a mathematical distinction between derivatives and partial derivatives. When we have a function of two variables, like US(p,q), the derivative isn't uniquely defined unless we specify a particular direction in the (p,q) plane. So we restrict the (p,q) plane to a particular curve, and find the slope along that curve. The partial derivative is the slope along a p=constant curve. But here I take the derivative along the demand curve.
Sunday, November 17, 2013
In which I think about supply and demand
Note: this post makes use of $\LaTeX$. That means it requires javascript, and cannot be viewed in a reader.
Earlier, I was entertained by learning a little bit about monopoly and monopsony. I know I am very ignorant of economics, and that this is pretty basic stuff. But perhaps readers can gain some insight by watching me learn things for the first time. Or if there is no insight to be gained by my readers, at least I benefit from the writing.
I read about monopoly and monopsony on Wikipedia. My instinct as a physicist is to (initially) ignore all real-world details and understand the simplest and most abstract problem. So of course I go straight to the graphs.
Figure 1: Monopoly
Figure 2: Monopsony
1. It seems the axes are backwards. It seems like prices are the independent variable, and the quantity of trades is the dependent variable, yet prices are on the vertical axis, while quantity is on the horizontal.
2. I thought a "competitive market" leads to the quantity (Qc) and price (Pc) at the intersection of the supply (S) and demand (D) curves. And yet in Figure 1, it's at the intersection of marginal cost (MC) and demand (D), while in Figure 2, it's at the intersection of supply (S) and marginal revenue product (MRP).
3. Under monopoly conditions, the quantity (Qm) is instead at the intersection of the marginal cost (MC) and marginal revenue (MR). Under monopsony conditions, the quantity is at the intersection of marginal cost (MC) and marginal revenue product (MRP). What's confusing is that marginal cost (Fig 1) and marginal cost (Fig 2) are completely different, even though they have the same name.
Explanations from Wikipedia were not forthcoming, because for some reason there's more emphasis on real world examples rather than mathematical abstractions. It's cool though, because I can do the math myself.
Perhaps more fundamental than the supply and demand curves, are the utility functions of the buyers and sellers, which I'll call UB and US respectively. These are functions of both quantity (q) and price (p). US is related to the cost of producing q units, which I'll call C(q). $$\text{US}(p,q) = pq - C(q)$$ Similarly, UB is related to V(q), the value of having q units. $$\text{UB}(p,q) = V(q) - pq$$ The supply curve tells you how many products the industry is willing to sell, given a certain price point. Basically, the supply is equal to the quantity such that US is maximized. The demand curve tells you how many products consumers are willing to buy, given a certain price point. Basically, the demand is equal to the quantity such that UB is maximized. In mathematical terms,
$$ S(p)=q|_{\frac{\partial \mathrm{US}(p,q) }{\partial q}=0}$$ $$D(p)=q|_{\frac{\partial \text{UB}(p,q)}{\partial q}=0}$$ from which we can derive $$\frac{dC}{dq}(S(p)) = p$$ $$\frac{dV}{dq}(D(p)) = p$$ $\frac{dC}{dq}$ is of course the marginal cost (MC in figure 1). So that means the marginal cost function is the inverse of the supply function. If you plot them on the graph, they will be the same curve. (People who aren't math purists might say they are in fact the same function.) $ \frac{dV}{dq}$ is the marginal value (which in the context of employers buying labor, is called marginal revenue product, MRP in figure 2). Since the marginal value is the inverse of the demand function they will also be the same curve on a graph.
This solves my confusion on points 1 and 2. While supply and demand are naturally functions of price, marginal cost and marginal value are naturally functions of quantity, so it makes sense to put quantity on the horizontal axis. And in both figures, the competitive market rate is in fact at the intersection of the supply and demand curves, even if the curves are not labeled as such.
This post is too long, so I will break here. Next time, I will talk about why a monopolistic market is different from a competitive market, and also "deadweight loss".
Thursday, November 14, 2013
Things I don't understand: health insurance
This will not be an intelligent post. I do not have intelligent things to say about health insurance.. I do not understand health insurance: what is good about it, what is bad, and the impact of various policies. I am also unable to make sense of what the internet tells me about health insurance.
Health insurance costs money, and what it gives in return is money. But if that were all, it seems like you can't really win against an insurance company that is still in business. Why is insurance ever worth it?
Most insurance is about reduction of risk. If you don't have homeowner's insurance, a house flood could financially ruin you. But if the cost of home repairs were spread out over all possible worlds, it might be easier to handle, even if there is some overhead going to an insurance company.
Of course, there's always this problem where different people have different levels of risk. Either there ends up being price discrimination, or insurance becomes too expensive for people with low risk, or insurers refuse to sell to people with high risk. I think Obamacare is meant to solve this problem by encouraging everyone to buy healthcare regardless of their level of risk, and by putting restrictions on price discrimination.
Although it also seems that risk reduction is not the only function of health insurance. Why does health insurance pay for regular check-ups, and why is it so expensive to pay for health care independently?
Maybe it's a little like restaurants. In theory, restaurants should be cheaper than cooking at home, because they benefit from economies of scale. In practice, restaurants are often more expensive because they offer service, space, and food quality. The economy of scale, the service, the space, and the food quality often come in the same package because it's efficient to do it that way. Perhaps the same is true of health insurance: risk reduction and regular check-ups come in the same package because it's efficient to do it that way. I'm not sure why though.
One idea is that preventative screenings are cost-efficient, but people irrationally avoid them because they cost money now. By reducing the marginal cost of preventative screenings, health insurers actually make health care cheaper by bypassing a psychological obstacle.
Another idea is that health insurers are able to allocate people to doctors or health care providers more efficiently than independent buyers of health care. Or they reduce administration costs.
One last idea is that health insurers create a monopsony, which is like a monopoly except instead of one seller, there is one buyer. Because there are fewer health insurers than people, they have more power to tell health care providers to lower their prices. I barely understand how a monopsony works, but it causes prices be lower than the "efficient" market value, whatever that means. It seems to me that the more of a monopsony there is for health care, the more of a monopoly there is for health insurance, and I don't understand how those things interact.
Many progressives advocate going further than Obamacare, adopting a "single-payer" system. I don't understand what the impact of this would be. I guess it would create more of a monopsony? People on the internet say it will reduce administration costs.
Dear readers, do you understand health insurance, or no?
Health insurance costs money, and what it gives in return is money. But if that were all, it seems like you can't really win against an insurance company that is still in business. Why is insurance ever worth it?
Most insurance is about reduction of risk. If you don't have homeowner's insurance, a house flood could financially ruin you. But if the cost of home repairs were spread out over all possible worlds, it might be easier to handle, even if there is some overhead going to an insurance company.
Of course, there's always this problem where different people have different levels of risk. Either there ends up being price discrimination, or insurance becomes too expensive for people with low risk, or insurers refuse to sell to people with high risk. I think Obamacare is meant to solve this problem by encouraging everyone to buy healthcare regardless of their level of risk, and by putting restrictions on price discrimination.
Although it also seems that risk reduction is not the only function of health insurance. Why does health insurance pay for regular check-ups, and why is it so expensive to pay for health care independently?
Maybe it's a little like restaurants. In theory, restaurants should be cheaper than cooking at home, because they benefit from economies of scale. In practice, restaurants are often more expensive because they offer service, space, and food quality. The economy of scale, the service, the space, and the food quality often come in the same package because it's efficient to do it that way. Perhaps the same is true of health insurance: risk reduction and regular check-ups come in the same package because it's efficient to do it that way. I'm not sure why though.
One idea is that preventative screenings are cost-efficient, but people irrationally avoid them because they cost money now. By reducing the marginal cost of preventative screenings, health insurers actually make health care cheaper by bypassing a psychological obstacle.
Another idea is that health insurers are able to allocate people to doctors or health care providers more efficiently than independent buyers of health care. Or they reduce administration costs.
One last idea is that health insurers create a monopsony, which is like a monopoly except instead of one seller, there is one buyer. Because there are fewer health insurers than people, they have more power to tell health care providers to lower their prices. I barely understand how a monopsony works, but it causes prices be lower than the "efficient" market value, whatever that means. It seems to me that the more of a monopsony there is for health care, the more of a monopoly there is for health insurance, and I don't understand how those things interact.
Many progressives advocate going further than Obamacare, adopting a "single-payer" system. I don't understand what the impact of this would be. I guess it would create more of a monopsony? People on the internet say it will reduce administration costs.
Dear readers, do you understand health insurance, or no?
Monday, November 11, 2013
Thoughts on gamer shame
When I went to the Queerness in Gaming Conference, a couple speakers made an analogy between the shame people feel for being queer, and the shame they feel for spending too much time playing video games.
This analogy is sort of a rhetorical trick. Everyone in the audience already considers queer shame to be mostly bad or unjustified, and the analogy frames the conversation such that we automatically think gamer shame must be equally bad or unjustified. Nonetheless, I find it to be a good analogy, because it draws "gamer shame" to our attention, and gets us to think critically about it.
Upon reflection, gamer shame is something that has long been present in my life, without me really thinking about it. I think it's the way I was brought up: my parents always tried to put a limit on how much games me and my brothers played. Now I replicate those same attitudes towards myself, and towards my boyfriend as well. Not without my boyfriend's permission of course--he knows he lacks a bit of self control, and that social encouragement is helpful to him.
Gamer shame also comes with a stereotype: the unhygienic middle aged man who still lives in his parents' basement, and plays WoW all day and night. The speakers made the interesting observation that when people try to show the positive face of gaming, they usually show people playing with friends on a couch. This image says, "Gaming is a social activity for socially functional human beings." It's as if gaming is only acceptable when it's on-the-couch multiplayer, and any form of solo gaming is unacceptable. We can draw a comparison to the way the image used to advocate gay rights is white gender-conforming men in long-term monogamous relationships.
I happen to like on-the-couch multiplayer games a lot, since that's what I would always play with my brothers growing up. But it's not as if I don't also play games solo. The fact that one is more socially acceptable than the other seems ridiculous. Most other media are also consumed alone. We read books alone. We listen to music alone. We watch TV alone. Movies are often thought of as a social outing, but it's not as if people interact with each other much while they're in a theater.
In general, I think it is good to think of gaming as just another medium. Spending time on video games is no less worthwhile than reading a novel or watching a movie.
At the same time, gaming is a very unique medium (as all media are unique). One thing that's very different about video games from other media is that length is usually a selling point. By contrast, when's the last time a movie was ever advertised as being very long? I think this is because video gaming often serves the function of killing time, and serves it well. Video games are usually built to be engaging, compelling, or hard to quit. This is a great thing, but can also lead to conflicts between what someone wants in the long term and in the short term. I don't know that "gamer shame" is justified, but surely "gamer self-control" has its uses.
This analogy is sort of a rhetorical trick. Everyone in the audience already considers queer shame to be mostly bad or unjustified, and the analogy frames the conversation such that we automatically think gamer shame must be equally bad or unjustified. Nonetheless, I find it to be a good analogy, because it draws "gamer shame" to our attention, and gets us to think critically about it.
Upon reflection, gamer shame is something that has long been present in my life, without me really thinking about it. I think it's the way I was brought up: my parents always tried to put a limit on how much games me and my brothers played. Now I replicate those same attitudes towards myself, and towards my boyfriend as well. Not without my boyfriend's permission of course--he knows he lacks a bit of self control, and that social encouragement is helpful to him.
Gamer shame also comes with a stereotype: the unhygienic middle aged man who still lives in his parents' basement, and plays WoW all day and night. The speakers made the interesting observation that when people try to show the positive face of gaming, they usually show people playing with friends on a couch. This image says, "Gaming is a social activity for socially functional human beings." It's as if gaming is only acceptable when it's on-the-couch multiplayer, and any form of solo gaming is unacceptable. We can draw a comparison to the way the image used to advocate gay rights is white gender-conforming men in long-term monogamous relationships.
I happen to like on-the-couch multiplayer games a lot, since that's what I would always play with my brothers growing up. But it's not as if I don't also play games solo. The fact that one is more socially acceptable than the other seems ridiculous. Most other media are also consumed alone. We read books alone. We listen to music alone. We watch TV alone. Movies are often thought of as a social outing, but it's not as if people interact with each other much while they're in a theater.
In general, I think it is good to think of gaming as just another medium. Spending time on video games is no less worthwhile than reading a novel or watching a movie.
At the same time, gaming is a very unique medium (as all media are unique). One thing that's very different about video games from other media is that length is usually a selling point. By contrast, when's the last time a movie was ever advertised as being very long? I think this is because video gaming often serves the function of killing time, and serves it well. Video games are usually built to be engaging, compelling, or hard to quit. This is a great thing, but can also lead to conflicts between what someone wants in the long term and in the short term. I don't know that "gamer shame" is justified, but surely "gamer self-control" has its uses.
Sunday, November 10, 2013
Solutions: Don't step on the grass
See the original problem
The "Don't step on the grass" puzzle was something I saw once, but at first I couldn't find it. It turns out it came from Wu : Riddles, under the header "Samwise and Gandalf". It involves Samwise trying to dig up a telephone line being used by Lord Sauron. My flavor text is much more banal in comparison.
I was surprised at the depth of this puzzle. Not only was every initial solution I found wrong, but so was every second solution. Here I'll show some of the suboptimal solutions. (The final solutions will be hidden as spoilers.) Below each solution is the length of fence, assuming that the polygon has unit sides.
My first solution was to have an X across the square.
This of course suggested radially symmetric solutions. So I looked for the best radially symmetric solutions for the pentagon and hexagon. For the pentagon, this involved a tricky geometric construction which I show below (the circle crosses the center of the pentagon, and line segments are colinear with the centers of circles).
Commenter Secret Squirrel found better solutions, so I immediately realized that radial symmetry was a bad constraint. I soon found the following solutions.
Finding that square solution was a breakthrough, because it made me realize the importance of 120 degree angles. To make a physics analogy, it's like you have bubbles. Bubbles shape themselves to minimize surface area. If three bubbles are adjacent to each other, they'll form flat surfaces with 120 degree angles. This led to an improvement in the pentagon solution.
I also found another solution to the pentagon, which is not quite as good. Also, commenter Rain found a solution for the square which was 2+1/sqrt(2).
Even though the above two solutions are excellent, they could still be improved with 120 degree angles. The hexagon solution was the right idea, but could be improved with a little rearrangement. Here are the final solutions:
The "Don't step on the grass" puzzle was something I saw once, but at first I couldn't find it. It turns out it came from Wu : Riddles, under the header "Samwise and Gandalf". It involves Samwise trying to dig up a telephone line being used by Lord Sauron. My flavor text is much more banal in comparison.
I was surprised at the depth of this puzzle. Not only was every initial solution I found wrong, but so was every second solution. Here I'll show some of the suboptimal solutions. (The final solutions will be hidden as spoilers.) Below each solution is the length of fence, assuming that the polygon has unit sides.
My first solution was to have an X across the square.
Square: 2*sqrt(2) = 2.828
This of course suggested radially symmetric solutions. So I looked for the best radially symmetric solutions for the pentagon and hexagon. For the pentagon, this involved a tricky geometric construction which I show below (the circle crosses the center of the pentagon, and line segments are colinear with the centers of circles).
Hexagon: 6*sqrt(3)/2 = 5.196
Pentagon: 4.396
Commenter Secret Squirrel found better solutions, so I immediately realized that radial symmetry was a bad constraint. I soon found the following solutions.
square: 1+sqrt(3) = 2.732
pentagon: 3.728
hexagon: 4.5
hexagon: 4.5
Finding that square solution was a breakthrough, because it made me realize the importance of 120 degree angles. To make a physics analogy, it's like you have bubbles. Bubbles shape themselves to minimize surface area. If three bubbles are adjacent to each other, they'll form flat surfaces with 120 degree angles. This led to an improvement in the pentagon solution.
Pentagon: 3.580
I also found another solution to the pentagon, which is not quite as good. Also, commenter Rain found a solution for the square which was 2+1/sqrt(2).
Pentagon: 3.588
Square: 2+1/sqrt(2) = 2.707
Even though the above two solutions are excellent, they could still be improved with 120 degree angles. The hexagon solution was the right idea, but could be improved with a little rearrangement. Here are the final solutions:
Square: sqrt(2)+sqrt(6)/2 = 2.639
Pentagon: 3.544
Hexagon: 1+sqrt(3)*2 = 4.464
Wednesday, November 6, 2013
Morality and game theory
I'm rather busy with work right now, so maybe now's a good time to ramble about not-fully-formed thoughts. This kind of writing takes less effort because I don't need to do research for it, and readers are invited to do most of the thinking.
In Sam Harris' book, The Moral Landscape, the eponymous landscape is basically a metaphor for a utility function. If we as a society make certain choices, that will put us somewhere on this landscape, and our height determines how good the outcome is. To Sam Harris, morality means finding the highest peaks on the landscape, and going there.
Sam Harris' metaphor exemplifies the view that morality is a calculation. Figure out what we want, figure out the best way to achieve it, and that's moral.
In everyday practice, morality often seems to serve a different function. Here are actions I do on a regular basis that I consider to have moral character: I clean dishes after using them, instead of leaving the task to others. I try to recycle as much as possible. I try to be polite and make my coworkers feel comfortable. All of these I do not because they benefit me, but primarily because they benefit others.
The fact of the matter is that we are always trapped in prisoner's dilemma (or similar games) of varying sizes. If I didn't wash the dishes, that would save me time, but cause more work for others. If none of us washed dishes, the sink would get dirty. Appealing to morality is a way to motivate people to cooperate. If someone doesn't cooperate, morality also offers us a mechanism to punish or shame them.
Now the tricky thing is, cooperation is not moral in every prisoner's dilemma. Here are some examples:
1. It is not moral for corporations to cooperate with each other by raising prices together. This can be argued from a utilitarian perspective, since the cooperation helps corporations, but causes greater harm to consumers.
2. Often it's not morally obligatory to give up property or our self-autonomy just because it might help someone else. We tend to place special value on rights like these.
3. We don't consider it immoral for a nation to have a military. If every nation has a military of equal strength, this is worse than the world where no one wastes resources on it. Yet the world where no nation has a military is unrealistic, so we don't expect nations to be cooperative to that degree.
Can you think of other situations where cooperation in prisoner's dilemma is not necessarily moral?
In Sam Harris' book, The Moral Landscape, the eponymous landscape is basically a metaphor for a utility function. If we as a society make certain choices, that will put us somewhere on this landscape, and our height determines how good the outcome is. To Sam Harris, morality means finding the highest peaks on the landscape, and going there.
Sam Harris' metaphor exemplifies the view that morality is a calculation. Figure out what we want, figure out the best way to achieve it, and that's moral.
In everyday practice, morality often seems to serve a different function. Here are actions I do on a regular basis that I consider to have moral character: I clean dishes after using them, instead of leaving the task to others. I try to recycle as much as possible. I try to be polite and make my coworkers feel comfortable. All of these I do not because they benefit me, but primarily because they benefit others.
The fact of the matter is that we are always trapped in prisoner's dilemma (or similar games) of varying sizes. If I didn't wash the dishes, that would save me time, but cause more work for others. If none of us washed dishes, the sink would get dirty. Appealing to morality is a way to motivate people to cooperate. If someone doesn't cooperate, morality also offers us a mechanism to punish or shame them.
Now the tricky thing is, cooperation is not moral in every prisoner's dilemma. Here are some examples:
1. It is not moral for corporations to cooperate with each other by raising prices together. This can be argued from a utilitarian perspective, since the cooperation helps corporations, but causes greater harm to consumers.
2. Often it's not morally obligatory to give up property or our self-autonomy just because it might help someone else. We tend to place special value on rights like these.
3. We don't consider it immoral for a nation to have a military. If every nation has a military of equal strength, this is worse than the world where no one wastes resources on it. Yet the world where no nation has a military is unrealistic, so we don't expect nations to be cooperative to that degree.
Can you think of other situations where cooperation in prisoner's dilemma is not necessarily moral?
Subscribe to:
Posts (Atom)
.jpg)